Effect of equivariance on training dynamics

Can relaxing equivariance help in finding better minima?

Group Equivariant Convolutional Network (G-CNN) has gained significant traction in recent years owing to their ability to generalize the property of CNNs being equivariant to translations in convolutional layers. With equivariance, the network is able to exploit groups of symmetries and a direct consequence of this is that it generally needs less data to perform well. However, incorporating such knowledge into the network may not always be advantageous, especially when the data itself does not exhibit full equivariance. To address this issue, the G-CNN was modified, introducing relaxed group equivariant CNNs (RG-CNN). Such modified networks adaptively learn the degree of equivariance imposed on the network, i.e. enabling it to operate on a level between full equivariance and no equivariance. Surprisingly, for rotational symmetries on fully equivariant data, found that a G-CNN exhibits poorer performance compared to a RG-CNN. This is a surprising result because a G-CNN, i.e. a fully equivariant network, is designed to perform well on fully equivariant data. Possibly the training dynamics benefit from relaxing of the equivariance constraint. To investigate this, we use the framework described in for measuring convexity and flatness using the Hessian spectra.

Inspired by the aforementioned observations, this blog post aims to answer the question: How does the equivariance imposed on a network affect its training dynamics? We identify the following subquestions:

  1. How does equivariance imposed on a network influence generalization?
  2. How does equivariance imposed on a network influence the convexity of the loss landscape?

We tackle these subquestions by analyzing trained models to investigate their training dynamics.

In view of space constraint, in this blogpost, we omit our reproducibility study and refer the readers to our extended blog post. Nevertheless, our reproducibility studies corroborated the following claims:

  1. Relaxed steerable G-CNN outperforms steerable G-CNN (fully equivariant network) on fully rotationally equivariant data as shown in the experiment on the super resolution dataset in .
  2. Relaxed G-CNN outperforms G-CNN on non-fully rotationally equivariant data as shown in the experiment on the smoke plume dataset in .

Background

Regular G-CNN

Consider the segmentation task depicted in the picture below.

Figure 1

Annotated segmented image taken from

Naturally, applying segmentation on a rotated 2D image should give the same segmented image as applying such rotation after segmentation. Mathematically, for a neural network $NN$ to be equivariant w.r.t. the group $(G,\cdot)$, such as 2D rotations, then the following property needs to be satisfied:

\[\begin{align*} NN (T_g x) = T'_g NN (x) & \qquad \qquad \forall g \in G. \\ \end{align*}\]

To build such a network, it is sufficient that each of its layers is equivariant in the same sense. Recall that a CNN achieves equivariance to translations by sharing weights in kernels that are translated across the input in each of its convolution layers. Hence, a G-CNN extends this concept of weight sharing to achieve equivariance w.r.t an arbitrary locally-compact group $G$.

For now on we will focus on affine groups, i.e., let $G := \mathbb{Z}^n \rtimes H$, where $H$ can be, for example, the rotation subgroup $SO(n)$ and $\mathbb{Z}^n$, the discrete translation group.

Furthermore, we’ll consider an input signal of $c_0$ channels on an $n$-dimensional grid $f_0: \mathbb{Z}^n \rightarrow \mathbb{R}^{c_0}$, e.g. RGB images ($f: \mathbb{Z}^2 \rightarrow \mathbb{R}^3$ ).

Lifting convolution

The first layer of a G-CNN lifts the input signal $f_0$ to the group $G$ using the kernel $\psi : \mathbb{Z}^n \rightarrow \mathbb{R}^{c_1 \times c_0}$ as follows:

\[(f_0 \star \psi)(\mathbf{x}, h) = \sum_{\mathbf{y} \in \mathbb{Z}^n} f_0(\mathbf{y}) \psi(h^{-1}(\mathbf{y} - \mathbf{x}))\]

where $\mathbf{x} \in \mathbb{Z}^n$ and $h \in H$. This yields $f_1: \mathbb{Z}^n \times H \rightarrow \mathbb{R}^{c_1}$ which is fed to the next layer.

$G$-equivariant convolution

Then, $f_1$ undergoes $G$-equivariant convolution with a kernel $\Psi: G \rightarrow \mathbb{R}^{c_2 \times c_1}$:

\[(f_1 \star \Psi)(\mathbf{x}, h) = \sum_{\mathbf{y} \in \mathbb{Z}^n} \sum_{h' \in H} f_1(\mathbf{y}, h') \Psi(h^{-1}(\mathbf{y} - \mathbf{x}), h^{-1}h')\]

where $\mathbf{x} \in \mathbb{Z}^n$ and $h \in H$. This outputs the signal $f_2: \mathbb{Z}^n \times H \rightarrow \mathbb{R}^{c_2}$. This way of convolving is repeated for all subsequent layers until the final aggregation layer, e.g. linear layer, if there is one.

Note that for regular group convolution to be practically feasible, $G$ has to be finite or addecuatly subsampled. Some of these limitations can be solved by steerable group convolutions.

Steerable G-CNN

First, consider the group representations $\rho_{in}: H \rightarrow \mathbb{R}^{c_\text{in} \times c_\text{in}}$ and $\rho_{out}: H \rightarrow \mathbb{R}^{c_\text{out} \times c_\text{out}}$. To address the aforementioned equivariance problem, $G$-steerable convolution modifies $G$-equivariant convolution with the following three changes:

To secure kernel $\psi$ has the mentioned property, we precompute a set of non-learnable basis kernels $(\psi_l)_{l=1}^L$ which do have it, and define all other kernels as weighted combinations of the basis kernels, using learnable weights with the same shape as the kernels.

Therefore, the convolution is of the form:

\[(f \star_{\mathbb{Z}^n} \psi) (\mathbf{x}) = \sum_{\mathbf{y} \in \mathbb{Z}^n} \sum_{l=1}^L (w_l ⊙ \psi_l(\mathbf{y}))f(\mathbf{x}+\mathbf{y})\]

Whenever both $\rho_{in}$ and $\rho_{out}$ can be decomposed into smaller building blocks called irreducible representations, equivariance w.r.t. infinite group $G$ is achieved (see Appendix A.1 of ).

Relaxed G-CNN

The desirability of equivariance in a network depends on the amount of equivariance possessed by the data of interest. To this end, relaxed G-CNN is built on top of a regular G-CNN using a modified (relaxed) kernel consisting of a linear combination of standard G-CNN kernels $ \{\Psi_l \}_1^{L} $. Consider $G := \mathbb{Z}^n \rtimes H$. Then, relaxed G-equivariant group convolution is defined as:

\[(f\;\tilde{\star}\;\Psi)(\mathbf{x}, h) = \sum_{\mathbf{y} \in \mathbb{Z}^n}\sum_{h' \in H} f(\mathbf{y}, h') \sum_{l=1}^L w_l(h) \Psi_l(h^{-1}(\mathbf{y} - \mathbf{x}), h^{-1} h')\]

or equivalently as a linear combination of regular group convolutions with different kernels:

\[\begin{aligned} (f\;\tilde{\star}\;\Psi)(\mathbf{x}, h) &= \sum_{l=1}^L w_l(h) \sum_{\mathbf{y} \in \mathbb{Z}^n}\sum_{h' \in H} f(\mathbf{y}, h') \Psi_l(h^{-1}(\mathbf{y} - \mathbf{x}), h^{-1} h')\\ &= \sum_{l=1}^L w_l(h) [(f \star \Psi_l)(\mathbf{x}, h)] \end{aligned}\]

This second formulation makes for a more interpretable visualization, as one can see in the following figure. There, one can observe how a network might learn to downweight the feature maps corresponding to 180 degree rotations, thus breaking rotational equivariance and allowing for different processing of images picturing 6s and 9s.

Visualization of relaxed lifting convolutions ($L=1$) as template matching. An input image $f_\text{in}$ contains a pattern $e$ in different orientations, each of which is weighted differently by the model.

Relaxed steerable G-CNN

Relaxed steerable G-CNN modified steerable G-CNN in a similar manner. Again, let the kernel in convolution be a linear combination of other kernels, such that the weights used depend on the variable of integration, leading to loss of equivariance.

\[(f \;\tilde{\star}_{\mathbb{Z}^n} \;\psi) (\mathbf{x}) = \sum_{\mathbf{y} \in \mathbb{Z}^n} \sum_{l=1}^L (w_l(\mathbf{y}) ⊙ \psi_l(\mathbf{y}))f(\mathbf{x}+\mathbf{y})\]

Furthermore, introduces a regularization term to impose equivariance on both relaxed models mentioned above. In our experiments, however, the best-performing models were those without this term.

Methodology

Datasets

Super-Resolution

The data consists of liquid flowing in 3D space and is produced by a high-resolution state-of-the-art simulation hosted by the John Hopkins University . Importantly, this dataset is forced to be isotropic, i.e. fully equivariant to rotations, by design.

For the experiment, a subset of 50 timesteps are taken, each downsampled from $1024^3$ to $64^3$ and processed into a task suitable for learning. The model is given an input of 3 consecutive timesteps, $t, t+1, t+2$ (which are first downsampled to $16^3$), and is tasked to upsample timestep $t+1$ to $64^3$, see Figure 1 for a visualization.

We use the following $3$ models from ’s experiment on the same dataset in Results:

Figure 1

Figure 1: Super Resolution architecture, taken from [1].

Smoke Plume

This is a synthetic $64 \times 64$ 2D smoke simulation dataset generated by PhiFlow , where dispersion of smoke in a scene starting from an inflow position with a buoyant force is simulated (Figure 2).

The dataset we used has a fixed inflow with buoyant force only pointing in one of the following $4$ directions: upwards, downwards, left, or right. For our experiments we keep the buoyant force the same in all directions such that the data is fully equivariant w.r.t. $90$ degree rotations.

Figure 2

Figure 2: Example of a Smoke Plume sequence generated by PhiFlow.

The models trained on this dataset are tasked with predicting the upcoming frame based on the current one. We use the following $2$ models in Results:

Training Dynamics Evaluation

To assess the training dynamics of a network, we are interested in the final performance and the generalizability of the learned parameters, which are quantified by the final RMSE, and the sharpness of the loss landscape near the final weight-point proposed in .

Sharpness

To measure the sharpness of the loss landscape after training, we consider changes in the loss averaged over random directions. Let $D$ denote a set of vectors randomly drawn from the unit sphere, and $T$ a set of displacements, i.e. real numbers. Then, the sharpness of the loss $\mathcal{L}$ at a point $w$ is:

\[\phi(w,D,T) = \frac{1}{|D||T|} \sum_{t \in T} \sum_{d \in D} |\mathcal{L}(w+dt)-\mathcal{L}(w)|\]

This definition is an adaptation from the one in . A sharper loss landscape around the model’s final weights usually implies a greater generalization gap.

Hessian Eigenvalue

Finally, the Hessian eigenvalue spectrum sheds light on both the efficiency and efficacy of neural network training. Negative Hessian eigenvalues indicate a non-convex loss landscape, which can disturb the optimization process, whereas very large eigenvalues indicate training instability, sharp minima and consequently poor generalization.

Results

In this section, we study how equivariance imposed on a network influences the convexity of the loss landscape and generalization, answering all the subquestions posed in Introduction.

Smoke Plume with full Equivariance

First, we examine the training, validation and test RMSE for the Steerable G-CNN (E2CNN) and Relaxed Steerable G-CNN (Rsteer) models on the fully equivariant Smoke Plume dataset.

Figure 5

Figure 5: Train RMSE curve for rsteer and E2CNN models

 Figure 6

Figure 6: Validation RMSE curve for rsteer and E2CNN models
Figure 7

Figure 7: Test RMSE for best models, averaged over five seeds

Figures 5 and 6 show the train and validation RMSE curves. While rsteer and E2CNN perform similarly on the training data, rsteer has lower RMSE on the validation data, indicating better generalization. Figure 7 confirms that rsteer performs best on the test set, consistent with results on the Isotropic Flow dataset in .

To understand why relaxed equivariant models outperform fully equivariant ones, we examine the sharpness of the loss and the Hessian spectra.

Figure 10

Figure 8: Sharpness at early and best epochs for rsteer and E2CNN models. On the equivariant Smokeplume dataset

Figure 10 shows that the rsteer model has much lower sharpness of the loss landscape compared to E2CNN for both checkpoints. This indicates a lower generalization gap, and thus more effective learning. This matches the lower validation RMSE curve we saw earlier.

A simple, elegant caption looks good between image rows, after each row, or doesn't have to be there at all.

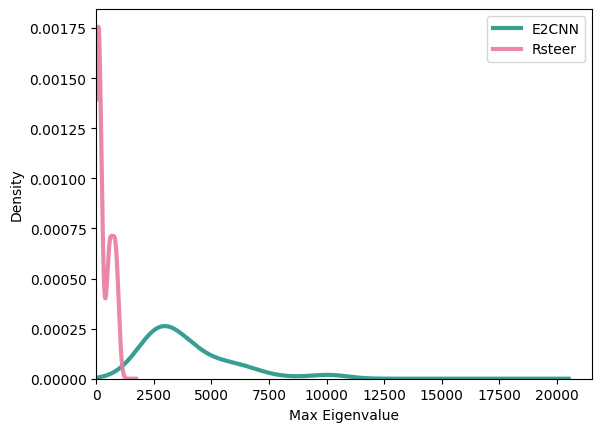
Figures 9 and 10 show Hessian spectra for the same checkpoints as the previous analysis. Regarding loss landscape flatness, both plots indicate that E2CNN has much larger eigenvalues than rsteer, potentially leading to training instability, less flat minima, and poor generalization for E2CNN.

To evaluate the convexity of the loss landscape, we examine the negative eigenvalues in the Hessian spectra. Neither model shows any negative eigenvalues, suggesting that both E2CNN and rsteer encounter convex loss landscapes. Therefore, convexity does not seem to significantly impact performance in this case.

Super Resolution

Similarly, we also analyze the training dynamics of the superresolution models on the isotropic Super-Resolution dataset.

First, we examine the training and validation MAE curves for the Relaxed Equivariant (RGCNN), Fully Equivariant (GCNN), and non-equivariant (CNN) models (run on 6 different seeds).

Figure 8

Figure 11: Training MAE curve for RGCNN, GCNN and CNN models

 Figure 9

Figure 12: Validation MAE curve for RGCNN, GCNN and CNN models

Here, we observe that early in the training (around epoch $3$), RGCNN starts outperforming the other two models and keeps this lead until its saturation at around $0.1$ MAE. For this reason, we take a checkpoint for each model on epoch $3$ (early) and on its best epoch (Best), to examine the corresponding sharpness values.

Figure 10

Figure 13: Sharpness of the loss landscape on the super resolution dataset. Ran over 6 seeds, error bars represent the standard deviation. For early, the third epoch was chosen, while for best the epoch with the best validation loss was chosen.

Figure 13 shows that the relaxed model has the lowest sharpeness in both cases. This indicates that the relaxed steerable GCNN has better generalisability during its training and at its convergence, matching our findings on the previous dataset.

Concluding Remarks

We reproduced and extended the relevant findings in reaffirming the effectiveness of relaxed equivariant models and demonstrating that they are able to outperform fully equivariant models even on perfectly equivariant datasets.

We furthermore investigated the authors’ speculation that this superior performance could be due to relaxed models having enhanced training dynamics. Our experiments empirically support this hypothesis, showing that relaxed models exhibit lower validation error, a flatter loss landscape around the final weights, and smaller Hessian eigenvalues, all of which are indicators of improved training dynamics and better generalization.

Our results suggest that replacing fully equivariant networks with relaxed equivariant networks could be advantageous in all application domains where some level of model equivariance is desired, including those where full equivariance is beneficial. For future research, we should investigate different versions of the relaxed model to find out which hyperparameters, like the number of filter banks, correlate with sharpness. Additionally, the method should be applied to different types of data to see if the same observations can be made there.

Code