Correct, Incorrect and Extrinsic Equivariance

What happens if we use an equivariant network when there is a mismatch between the model symmetry and the problem symmetry?

Abstract

Although equivariant machine learning has proven effective at many tasks, success depends heavily on the assumption that the ground truth function is symmetric over the entire domain matching the symmetry in an equivariant neural network. A missing piece in the equivariant learning literature is the analysis of equivariant networks when symmetry exists only partially or implicitly in the domain. We propose the definitions of correct, incorrect, and extrinsic equivariance, which describe the relationship between model symmetry and problem symmetry. We show that imposing extrinsic equivariance can improve the model’s performance. We also provide the lower error bound analysis of incorrect equivariance, quantitatively showing the degree to which the symmetry mismatch will impede learning.

Introduction

Equivariant Networks have shown great benefit for improving sample efficiency.

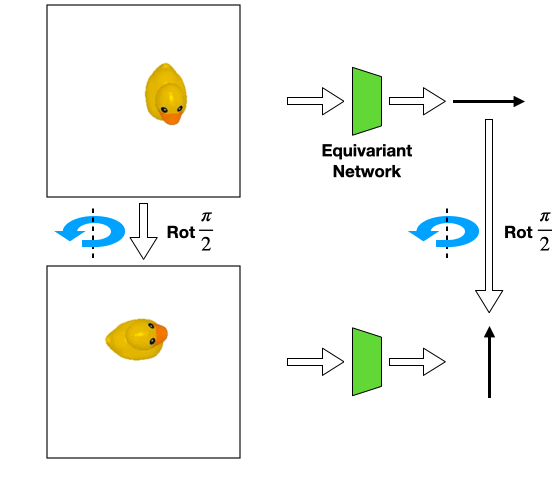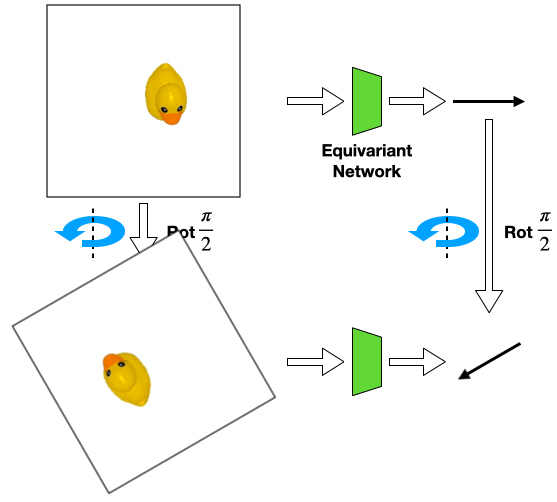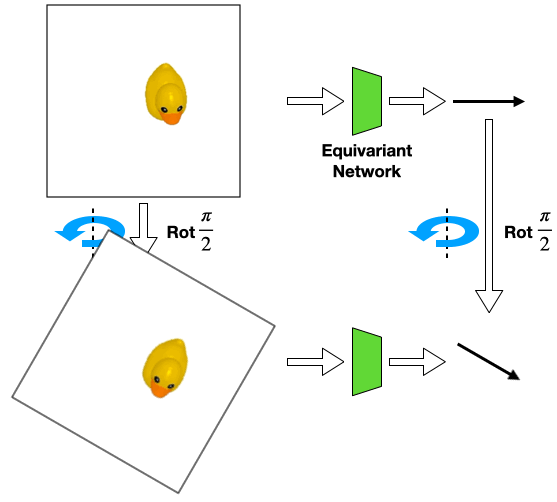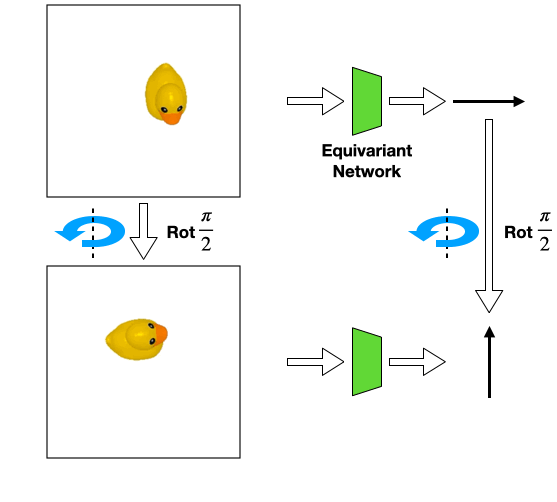
For example, consider the above position estimation task. We can use a rotationally equivariant network which will automatically generalize to different rotations of the same input. However, a perfect top-down image is normally required in order to model the problem symmetry as transformations of the input image.

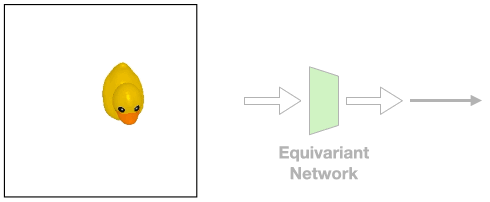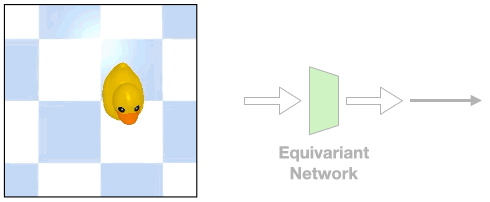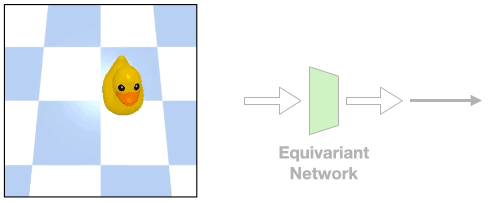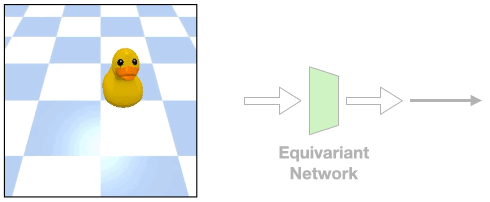
Such assumption can be easily violated in the real world where there could be a fixed background or a tilted view angle.

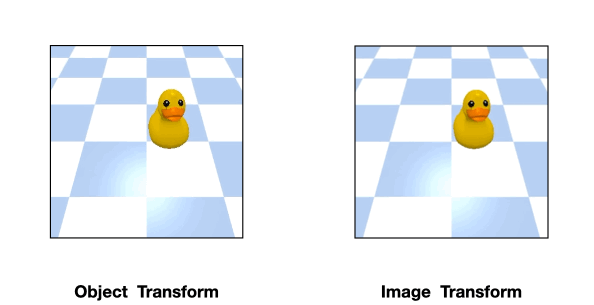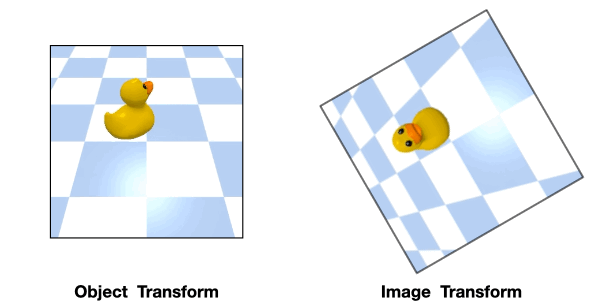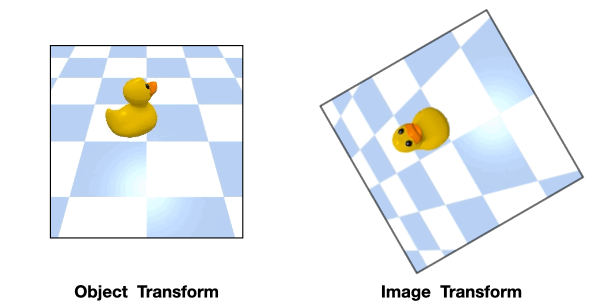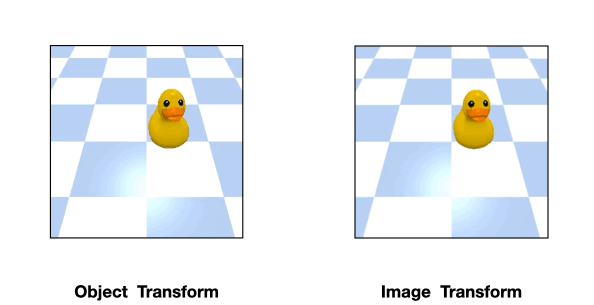
In these cases, the transformation of the object will be different from that of the image

Such object transformation will be hard to model and an equivariant network will not directly apply.

However, we can still use an equivariant network that encodes the image-wise symmetry instead. In this work, we study what will happen if we use equivariant networks under such symmetry-mismatch scenarios.

Correct, Incorrect, and Extrinsic Equivariance

We first define correct, incorrect, and extrinsic equivariance, three different relationships between model symmetry and problem symmetry.

Consider a classification task where the model needs to classify the blue and orange points in the plane.

If we enforce reflection symmetry across the horizontal axis, the transformed data under reflection will have the same color as the original data, so the model preserves the problem symmetry, and we call it correct equivariance.

If we enforce rotation symmetry by pi, the transformed data under the rotation will have different color as the original data, so the model will be forced to generate wrong answers, and we call it incorrect equivariance.

If we enforce scale symmetry, the transformed data under scaling will be outside of the input distribution shown in the gray ring, so we call it extrinsic equivariance.

Extrinsic Equivairance Helps Learning

We show that extrinsic equivariance can helps learning. Our hypothesis is that extrinsic equivariance can makes it easier for the network to generate the decision boundary.

We test our proposal in robotic manipulation (and in other domains, please see the paper ) using SO(2)-Equivariant SAC , but the observation is taken from a camera with a tilted view angle. This tilted view angle makes the symmetry extrinsic because a rotated image will be out-of-distribution. We show that the extrinsic equivariant methods (blue) significantly outperform the unconstrained baselines.

Lower Bound of Incorrect Equivariance

We futher analyze the lower bound of error caused by incorrect equivariance. Consider a digit classification task where we use a \(D_2\)-invariant network to classify digits.

For digit 2, a \(\pi\)-rotation symmetry is correct equivariance, while a vertical flip symmetry is incorrect (as it transforms 2 into a 5). For digit 3, a \(\pi\)-rotation symmetry is extrinsic (the rotated digit is out-of-distribution), while vertical flip symmetry is correct equivariance.

Let us focus on an image \(x\) of digit 2 first, we can get the orbit \(Gx\) with respect to the group \(G=D_2\).

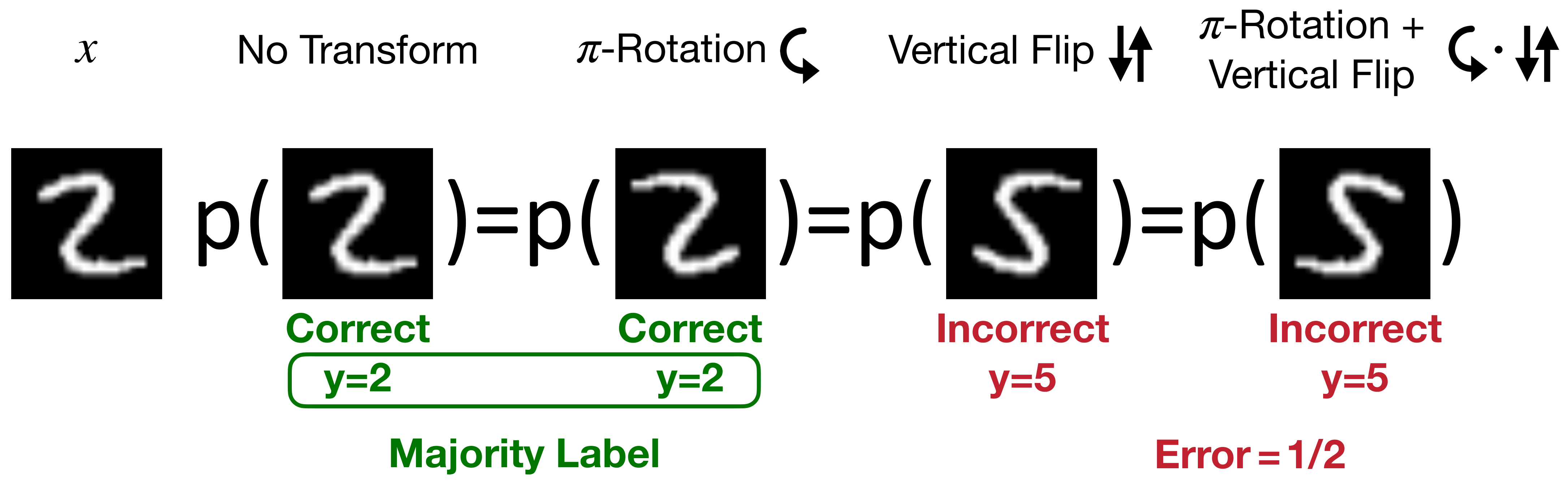
Inside the orbit, two elements will have correct equivariance, and two other elements will have incorrect equivariance. If we assume the probability \(p\) of all four images are identical, we can calculate the minimum error of a \(D_2\)-invariant network inside the orbit \(Gx\) as \(k(Gx)=\frac{1}{2}\).

Doing the same calculation for all digits, we can calculate the minimum error as the mean of all \(k(Gx)\).

Formally, we define \(k(Gx)\) as the total dissent of the orbit \(Gx\), which is the integrated probability density of the elements in the orbit having a different label than the majority label. The invariant classification is then lower bounded by the integral of rotal dissent over the fundamental domain \(F\).

We also analyze the lower bounds of invariant and equivariant regression, please see them in the paper .

Conclusion

In this work, we both theoretically and empirically study the use of equivariant networks under a mismatch between the model symmetry and the problem symmetry. We define correct, incorrect, and extrinsic equivariance, and show that while incorrect equivariance will create an error lower bound, extrinsic equivariance can aid learning. For more information, please checkout our full papers and .