Equivariant Diffusion for Molecule Generation in 3D using Consistency Models

Introduction to the seminal papers "Equivariant Diffusion for Molecule Generation in 3D" and "Consistency Models" with an adaptation fusing the two together for fast molecule generation.

Introduction

In this blog post, we discuss the paper “Equivariant Diffusion for Molecule Generation in 3D” , which first introduced 3D molecule generation using diffusion models. Their Equivariant Diffusion Model (EDM) also incorporated an Equivariant Graph Neural Network (EGNN) architecture, effectively grounding the model with inductive priors about the symmetries in 3D space. EDM demonstrated strong improvement over other (non-diffusion) generative methods for molecules at the time and inspired many further influential works in the field .

Most diffusion models are unfortunately bottle-necked by the sequential denoising process, which can be slow and computationally expensive . Hence, we also introduce “Consistency Models” and demonstrate that an EDM can generate samples up to 24x faster in this paradigm with as little as a single step. However, we unfortunately found the quality of samples generated by the consistency model to be much worse than from the original EDM.

Briefly on Equivariance for molecules

Equivariance is a property of certain functions, which ensures that their output transforms in a predictable manner under collections of transformations. This property is valuable in molecular modeling, where it can be used to ensure that the properties of molecular structures are consistent with their symmetries in the real world. Specifically, we are interested in ensuring that structure is preserved in the representation of a molecule under three types of transformations: translation, rotation, and reflection.

Formally, we say that a function $f$ is equivariant to the action of a group $G$ if:

\[\begin{align} T_g(f(x)) = f(S_g(x)) \end{align}\]

for all $g \in G$, where $S_g,T_g$ are linear representations related to the group element $g$ .

The three transformations: translation, rotation, and reflection, form the Euclidean group $E(3)$, which is the group of all aforementioned isometries in three-dimensional space, for which $S_g$ and $T_g$ can be represented by a translation $t$ and an orthogonal matrix $R$ that rotates or reflects coordinates.

A function $f$ is then equivariant to a rotation or reflection $R$ if transforming its input results in an equivalent transformation of its output :

\[\begin{align} Rf(x) = f(Rx) \end{align}\]

Introducing Equivariant Graph Neural Networks (EGNNs)

Molecules can very naturally be represented with graph structures, where the nodes are atoms and edges their bonds. The features of each atom, such as its element type or charge can be encoded into an embedding $\mathbf{h}_i \in \mathbb{R}^d$ alongside with the atoms 3D position $\mathbf{x}_i \in \mathbb{R}^3$.

To learn and operate on such structured inputs, Graph Neural Networks (GNNs) have been developed, falling under the message passing paradigm . This architecture consists of several layers, each of which updates the representation of each node, using the information in nearby nodes.

Figure 1: visualization of a message passing network

The previously mentioned $E(3)$ equivariance property of molecules can be injected as an inductive prior into to the model architecture of a message passing graph neural network, resulting in an $E(3)$ EGNN. This property improves generalisation and also beats similar non-equivariant Graph Convolution Networks on the molecular generation task .

The EGNN is built with equivariant graph convolution layers (EGCLs):

\[\begin{align} \mathbf{x}^{l+1},\mathbf{h}^{l+1}=EGCL[ \mathbf{x}^l, \mathbf{h}^l ] \end{align}\]

An EGCL layer can be formally defined by:

$$ \begin{align} \mathbf{m}_{ij} = \phi_e(\mathbf{h}_i^l, \mathbf{h}_j^l, d^2_{ij}) \end{align} $$ $$ \begin{align} \mathbf{h}_i^{l+1} = \phi_h\left(\mathbf{h}_i^l, \sum_{j \neq i} \tilde{e}_{ij} \mathbf{m}_{ij}\right) \end{align} $$ $$ \begin{align} \mathbf{x}_i^{l+1} = \mathbf{x}_i^l + \sum_{j \neq i} \frac{\mathbf{x}_i^l \mathbf{x}_j^l}{d_{ij} + 1} \phi_x(\mathbf{h}_i^l, \mathbf{h}_j^l, d^2_{ij}) \end{align} $$

where $h_l$ represents the feature $h$ at layer $l$, $x_l$ represents the coordinate at layer $l$ and $d_{ij}= ||x_i^l-x^l_j||_2$ is the Euclidean distance between nodes $v_i$ and $v_j$.

A fully connected neural network is used to learn the functions $\phi_e$, $\phi_x$, and $\phi_h$. At each layer, a message $m_{ij}$ is computed from the previous layer’s feature representation. Using the previous feature and the sum of these messages, the model computes the next layer’s feature representation.

This architecture then satisfies translation and rotation equivariance. Notably, the messages depend on the distance between the nodes and these distances are not changed by isometric transformations.

Equivariant Diffusion Models (EDM)

This section introduces diffusion models and describes how their predictions can be made $E(3)$ equivariant. The categorical properties of atoms are already invariant to $E(3)$ transformations, hence, we are only interested in enforcing this property on the sampled atom positions.

What are Diffusion Models?

Diffusion models are inspired by the principles of diffusion in physics, and model the flow of a data distribution to pure noise over time. A neural network is then trained to learn a reverse process that reconstructs samples on the data distribution from pure noise.

Figure 2: The Markov process of forward and reverse diffusion

The “forward” noising process can be parameterized by a Markov process , where transition at each time step $t$ adds Gaussian noise with a variance of $\beta_t \in (0,1)$:

\[\begin{align} q\left( x_t \mid x_{t-1} \right) := \mathcal{N}\left( x_t ; \sqrt{1-\beta_t} x_{t-1}, \beta_t \mathbf{I} \right) \end{align}\]

The whole Markov process leading to time step $T$ is given as a chain of these transitions:

\[\begin{align} q\left( x_1, \ldots, x_T \mid x_0 \right) := \prod_{t=1}^T q \left( x_t \mid x_{t-1} \right) \end{align}\]

The “reverse” process transitions are unknown and need to be approximated using a neural network parametrized by $\theta$:

\[\begin{align} p_\theta \left( x_{t-1} \mid x_t \right) := \mathcal{N} \left( x_{t-1} ; \mu_\theta \left( x_t, t \right), \Sigma_\theta \left( x_t, t \right) \right) \end{align}\]

Because we know the dynamics of the forward process, the variance $\Sigma_\theta \left( x_t, t \right)$ at time $t$ is known and can be fixed to $\beta_t \mathbf{I}$.

The predictions then only need to obtain the mean $\mu_\theta \left( x_t, t \right)$, given by:

\[\begin{align} \mu_\theta \left( x_t, t \right) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta\_t}{\sqrt{1 - \bar{\alpha}\_t}} \epsilon\_\theta \left( x_t, t \right) \right) \end{align}\]

where $\alpha_t = \Pi_{s=1}^t \left( 1 - \beta_s \right)$.

Hence, we can directly predict $x_{t-1}$ from $x_{t}$ using the network $\theta$:

\[\begin{align} x_{t-1} = \frac{1}{\sqrt{1 - \beta_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \alpha_t}} \epsilon_\theta \left( x_t, t \right) \right) + \sqrt{\beta_t} v_t \end{align}\]

where $v_T \sim \mathcal{N}(0, \mathbf{I})$ is a sample from the pure Gaussian noise.

Enforcing E(3) equivariant diffusion

Equivariance to rotations and reflections effectively means that if any orthogonal rotation matrix $\mathbf{R}$ is applied to a sample $\mathbf{x}_t$ at any given time step $t$, we should still generate a correspondingly rotated “next best sample” $\mathbf{R}\mathbf{x}_{t+1}$ at time $t+1$.

In other words, the likelihood of this next best sample does not depend on the molecule’s rotation and the probability distribution for each transition in the Markov Chain is hence roto-invariant:

\[\begin{align} p(y|x) = p(\mathbf{R}y|\mathbf{R}x) \end{align}\]

Figure 3: Examples of 2D roto-invariant distributions

Such an invariant distribution composed with an equivariant invertible function results in another invariant distribution . Furthermore, if $x \sim p(x)$ is invariant to a group, and the transition probabilities of a Markov chain $y \sim p(y|x)$ are equivariant, then the marginal distribution of $y$ at any time step $t$ is also invariant to that group .

Since the underlying EGNN already ensures this equivariance, the remaining constraint can easily be achieved by setting the initial sampling distribution to something roto-invariant, such as a simple mean zero Gaussian with a diagonal covariance matrix, as illustrated in Figure 3 (left).

Translation equivariance requires a few tricks. It has been shown, that it is impossible to have non-zero distributions invariant to translations . Intuitively, the translation invariance property means that any point $\mathbf{x}$ results in the same assigned $p(\mathbf{x})$, leading to a uniform distribution, which, if stretched over an unbounded space, would be approaching zero-valued probabilities thus not integrating to one.

The EDM authors bypass this with a clever trick of always re-centering the generated samples to have center of gravity at $\mathbf{0}$ and further show that these $\mathbf{0}$-centered distributions lie on a linear subspace that can reliably be used for equivariant diffusion .

How to train the EDM?

The training objective of diffusion-based generative models amounts to “maximizing the log-likelihood of the sample on the original data distribution.”

During training, a diffusion model learns to approximate the parameters of a posterior distributions at the next time step by minimizing the KL divergence between this estimate and the ground truth, which is equivalent objective to minimizing the negative log likelihood.

\[\begin{align} L_{vlb} := L_{t-1} := D_{KL}(q(x_{t-1}|x_{t}, x_{0}) \parallel p_{\theta}(x_{t-1}|x_{t})) \end{align}\]

The EDM adds a caveat that the predicted distributions must be calibrated to have center of gravity at $\mathbf{0}$, in order to ensure equivariance.

Using the KL divergence loss term with the EDM model parametrization simplifies the loss function to:

\[\begin{align} \mathcal{L}_t = \mathbb{E}_{\epsilon_t \sim \mathcal{N}_{x_h}(0, \mathbf{I})} \left[ \frac{1}{2} w(t) \| \epsilon_t - \hat{\epsilon}_t \|^2 \right] \end{align}\]

where $w(t) = \left(1 - \frac{\text{SNR}(t-1)}{\text{SNR}(t)}\right)$ and $\hat{\epsilon}_t = \phi(z_t, t)$.

The EDM authors found that the model performs best with a constant $w(t) = 1$, thus effectively simplifying the loss function to an MSE. Since coordinates and categorical features are on different scales, it was also found that scaling the inputs before inference and then rescaling them back also improves performance.

Consistency Models

As previously mentioned, diffusion models are bottlenecked by the sequential denoising process . Consistency Models reduce the number of steps during de-noising up to just a single step, significantly speeding up this costly process, while allowing for a controlled trade-off between speed and sample quality.

Modelling the noising process as an SDE

Song et al. have shown that the noising process in diffusion can be described with a Stochastic Differential Equation (SDE) transforming the data distribution $p_{\text{data}}(\mathbf{x})$ in time:

\[\begin{align} d\mathbf{x}_t = \mathbf{\mu}(\mathbf{x}_t, t) dt + \sigma(t) d\mathbf{w}_t \end{align}\]

Where $t$ is the time-step, $\mathbf{\mu}$ is the drift coefficient, $\sigma$ is the diffusion coefficient, and $\mathbf{w}_t$ is the stochastic component denoting standard Brownian motion. This stochastic component effectively represents the iterative adding of noise to the data in the forward diffusion process and dictates the shape of the final distribution at time $T$.

Typically, this SDE is designed such that $p_T(\mathbf{x})$ at the final time-step $T$ is close to a tractable Gaussian.

Figure 4: Illustration of a bimodal distribution evolving to a Gaussian over time

Existence of the PF ODE

This SDE has a remarkable property, that a special ODE exists, whose trajectories sampled at $t$ are distributed according to $p_t(\mathbf{x})$ :

\[\begin{align} d\mathbf{x}_t = \left[ \mathbf{\mu}(\mathbf{x}_t, t) - \frac{1}{2} \sigma(t)^2 \nabla \log p_t(\mathbf{x}_t) \right] dt \end{align}\]

This ODE is dubbed the Probability Flow (PF) ODE by Song et al. and corresponds to the different view of diffusion manipulating probability mass over time we hinted at in the beginning of the section.

A score model $s_\phi(\mathbf{x}, t)$ can be trained to approximate $\nabla log p_t(\mathbf{x})$ via score matching . Since we know the parametrization of the final distribution $p_T(\mathbf{x})$ to be a standard Gaussian parametrized with $\mathbf{\mu}=0$ and $\sigma(t) = \sqrt{2t}$, this score model can be plugged into the equation (16) and the expression reduces itself to an empirical estimate of the PF ODE:

\[\begin{align} \frac{dx_t}{dt} = -ts\phi(\mathbf{x}_t, t) \end{align}\]

With $\mathbf{\hat{x}}_T$ sampled from the specified Gaussian at time $T$, the PF ODE can be solved backwards in time to obtain a solution trajectory mapping all points along the way to the initial data distribution at time $\epsilon$ very close to zero.

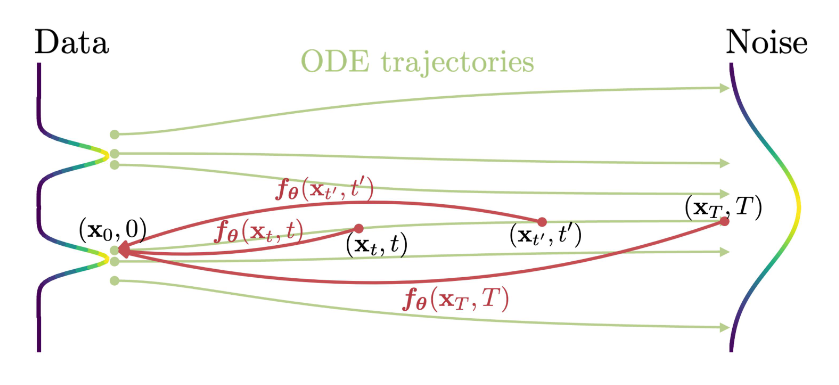
Figure 5: Solution trajectories of the PF ODE.

Given any off-the-shelf ODE solver (e.g. Euler) and a trained score model $s_\phi(\mathbf{x}, t)$, we can solve this PF ODE. The time horizon $[\epsilon, T]$ is discretized into sub-intervals for improved performance . A solution trajectory, denoted $\\{\mathbf{x}_t\\}$, is then given as a finite set of samples $\mathbf{x}_t$ for every discretized time-step $t$ between $\epsilon$ and $T$.

Consistency Function

Given a solution trajectory ${\mathbf{x}_t}$, we define the consistency function as:

\[\begin{align} f: (\mathbf{x}_t, t) \to \mathbf{x}_{\epsilon} \end{align}\]

In other words, for every pair ($\mathbf{x}_t$, $t$), a consistency function always outputs a corresponding datapoint at time $\epsilon$, which will be very close to the original data distribution.

Importantly, this function has the property of self-consistency: i.e. its outputs are consistent for arbitrary pairs of $(x_t, t)$ that lie on the same PF ODE trajectory. Hence, we have

\[f(x_t, t) = f(x_{t'}, t') \text{ for all } t, t' \in [\epsilon, T]\]

The goal of a consistency model, denoted by $f_\theta$, is to estimate this consistency function $f$ from data by being enforced with this self-consistency property during training.

Sampling

With a fully trained consistency model $f_\theta(\cdot, \cdot)$, we can generate new samples by simply sampling from the initial Gaussian $\hat{x_T}$ $\sim \mathcal{N}(0, T^2I)$ and propagating this through the consistency model to obtain samples on the data distribution $\hat{x_{\epsilon}}$ $= f_\theta(\hat{x_T}, T)$ with as little as one diffusion step.

Figure 6: Visualization of PF ODE trajectories for molecule generation in 3D.

Training Consistency Models

Consistency models can either be trained by “distillation” from a pre-trained diffusion model, or in “isolation” as a standalone generative model from scratch. In the context of our work, we focused only on the latter because the distillation approach has a hard requirement of using a pretrained score based diffusion. In order to train in isolation we need to leverage the following unbiased estimator:

\[\begin{align} \nabla \log p_t(x_t) = - \mathbb{E} \left[ \frac{x_t - x}{t^2} \middle| x_t \right] \end{align}\]

where $x \sim p_\text{data}$ and $x_t \sim \mathcal{N}(x; t^2 I)$.

That is, given $x$ and $x_t$, we can estimate $\nabla \log p_t(x_t)$ with $-(x_t - x) / t^2$. This unbiased estimate suffices to replace the pre-trained diffusion model in consistency distillation when using the Euler ODE solver in the limit of $N \to \infty$ .

Song et al. justify this with a further theorem in their paper and show that the consistency training objective (CT loss) can then be defined as:

\[\begin{align} \mathcal{L}_{CT}^N (\theta, \theta^-) &= \mathbb{E}[\lambda(t_n)d(f_\theta(x + t_{n+1} \mathbf{z}, t_{n+1}), f_{\theta^-}(x + t_n \mathbf{z}, t_n))] \end{align}\]

where $\mathbf{z} \sim \mathcal{N}(0, I)$.

Crucially, $\mathcal{L}(\theta, \theta^-)$ only depends on the online network $f_\theta$, and the target network $f_{\theta^-}$, while being completely agnostic to diffusion model parameters $\phi$.

Experiments

We replicate the original EDM set-up and evaluate on the QM9 dataset . Due to computational constraints and the demonstrational nature of this blogpost, we only trained models for 130 epochs with the default hyperparameter settings given by the original EDM implementation to illustrate the trade-offs in speed and quality of samples.

Model / Sampling Time (seconds)	Mean	STD
Default EDM	0.6160	0.11500
Consistency Model (single step)	0.0252	0.00488

Table 1: EDM and Consistency Model inference speed

As expected, we observed in table 1., that the consistency model in single-step mode is significantly faster than the EDM, providing up to a 24x speed-up averaged over 5 sampling runs. This number represents the time it takes the model to generate a sample on the data distribution from a pure Gaussian noise input, excluding other computational overheads shared by both models equally, such as logging.

Model / Metric	Training NLL	Validation NLL	Best Cross-Validated Test NLL	Best Atom Stability	Best Molecule Stability
Default EDM	2.524	-30.066	-17.178	0.873	0.196
Consistency Model (single step)	2.482	94176	80363	0.19	0
Consistency Model (multi-step)	2.484	166264	179003	0.12	0

Table 2: EDM and Consistency Model results on the QM9 dataset after 130 epochs.

We observed that the consistency models converge on the training set with similar rate as the regular EDM, even achieving slightly lower training NLLs. However, they completely fail to generalize to the validation and test sets with much lower atom stability (the proportion of atoms that have the right valency) and no molecule stability (the proportion of generated molecules for which all atoms are stable). These results are surprisingly poor, given that the dataset is not particularly complicated, and consistency models have already shown promising results on images and reportedly, shows competitive results on QM9 as well .

To improve these results, we attempted to use multi-step sampling, which should in theory allow us to replicate results close to the EDM with the same number of sampling steps. However, we observed no such improvement in our experiments. We tested multiple different amounts of steps and report results for 100, which performed best overall. Oddly, the multi-step sampling actually yields worse results than the single-step sampling most of the time, which is highly unexpected and requires further investigation.

It should also be noted that the default EDM with more training is capable of achieving results much better than what we report in table 2. However, it still comfortably outperforms all consistency model variations on all metrics using equal amounts of compute.

Discussion

Consistency models are able to reduce the number of steps during sampling up to just a single step, significantly speeding up the sampling process. We were able to successfully demonstrate this and train an EDM as a consistency model in isolation, achieving nearly identical training loss with up to 24x faster sampling times. However, using the single-step sampling only achieves up to 19% atom stability in best case scenario, compared with the default EDM which consistently reaches 87% or much more with further training. We suspect that a model trained in this set-up might be too prone to overfitting and struggles with generalization to anything outside the training data distribution, compared to sequential de-noising predictions of the EDM, which are more robust by design.

Using multi-step sampling should in theory yield competitive results, but we observed no such improvement. Since it cannot be conclusively ruled out that this was caused by a bug in our multi-step sampling code, we hope to continue investigating if the consistency model paradigm can reliably be used for molecule generation in the future and show more competitive results as previous works suggest is possible .