Equivariant Neural Fields - continuous representations grounded in geometry
An intro to geometry-grounded continuous signal representations and their use in modelling spatio-temporal dynamics.
Introduction
Neural fields (NeFs)
A major limitation of NeFs as representation is their lack of interpretibility and preservation of geometric information. In this blog post, we delve into the recent advancements presented in the paper “Grounding Continuous Representations in Geometry: Equivariant Neural Fields”
The Evolution of Neural Fields
Neural fields are functions that map spatial coordinates to feature representations. For instance, a neural field \(f_{\theta}: \mathbb{R}^d \rightarrow \mathbb{R}^c\) can map pixel coordinates \(x\) to RGB values to represent images. These fields are typically parameterized by neural networks, which are optimized to approximate a target signal \(f_\theta\) within a reconstruction task. Although this gives rise to continuous representations, for multiple signals, the weights \(\theta_f\) are optimized separately for each signal \(f\), leading to a lack of shared structure across different signals and the need to train different seperate models.
While this approach results in continuous representations, it also presents a significant drawback. For multiple signals, the weights \(\theta_f\) must be optimized separately for each signal \(f\) This leads to a lack of shared structure across different signals and necessitates training separate models for each individual signal.

Conditional Neural Fields (CNFs) extend this concept of neural fields by introducing a conditioning variable \(z_f\) that modulates the neural field for a specific signal \(f\). This enhancement allows CNFs to effectively represent an entire dataset of signals \(f \in \mathcal{D}\) using a single, shared set of weights \(\theta\) along with a set of unique conditioning variables \(z_f\). Since these representations are signal-specific, they latents can be used as a representation in downstream tasks. This approach has been successful in various tasks, including classification
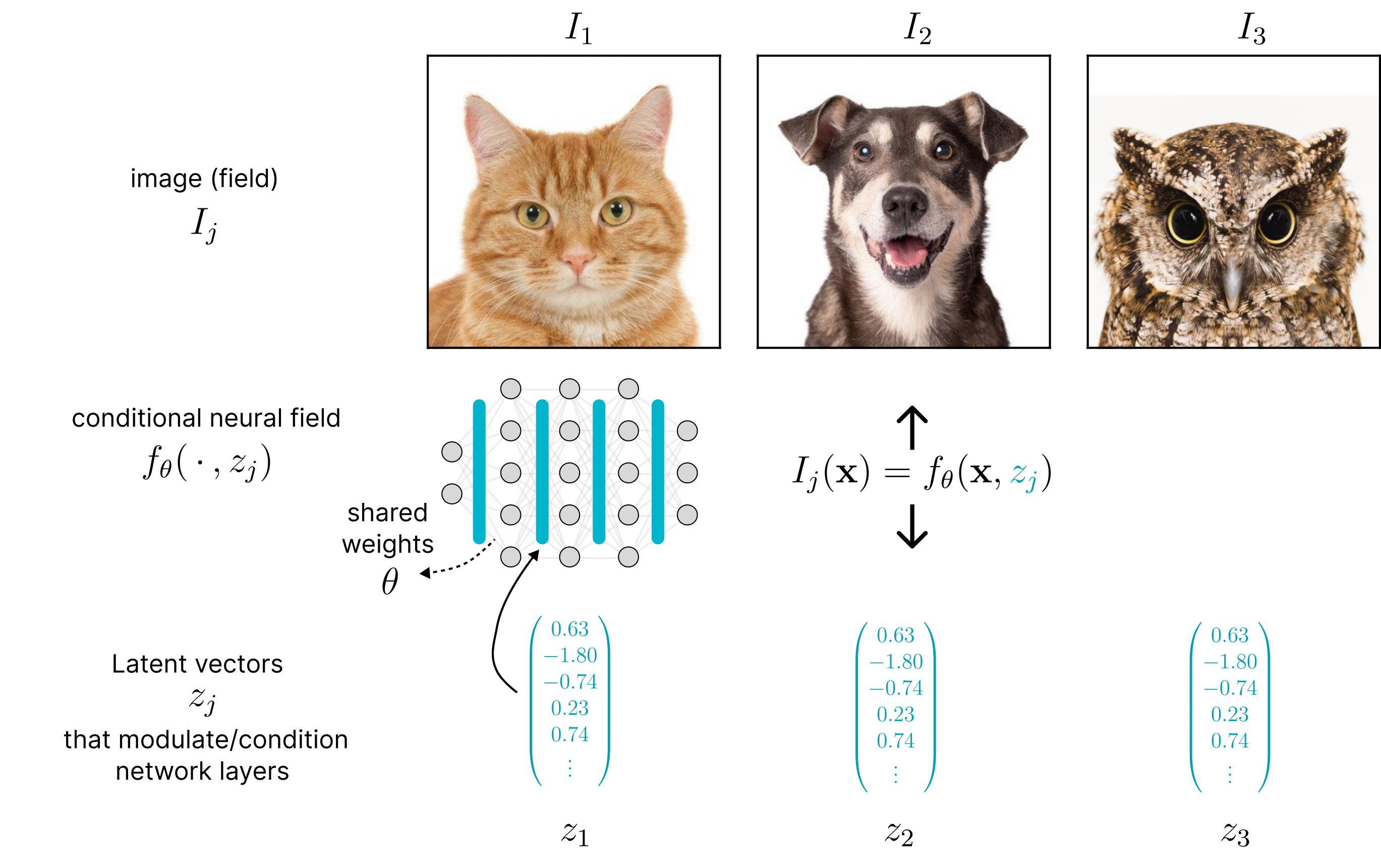
However, conventional CNFs often lack geometric interpretability, they are able to capture textures and appearances which is shown by their performance in reconstruction. However, they do struggle to encode explicit geometric information necessary for tasks requiring spatial reasoning. Think for example of simple geometric transformations like rotations or translations, which are not inherently captured by CNFs; it is unclear how these transformations would manifest in the latent space.
Introducing Equivariant Neural Fields
Equivariant Neural Fields (ENFs) address this limitation by grounding neural field representations in geometry. ENFs use latent point clouds as conditioning variables, where each point is a tuple consisting of a pose and a context vector. This grounding ensures that transformations in the field correspond to transformations in the latent space, a property known as equivariance.
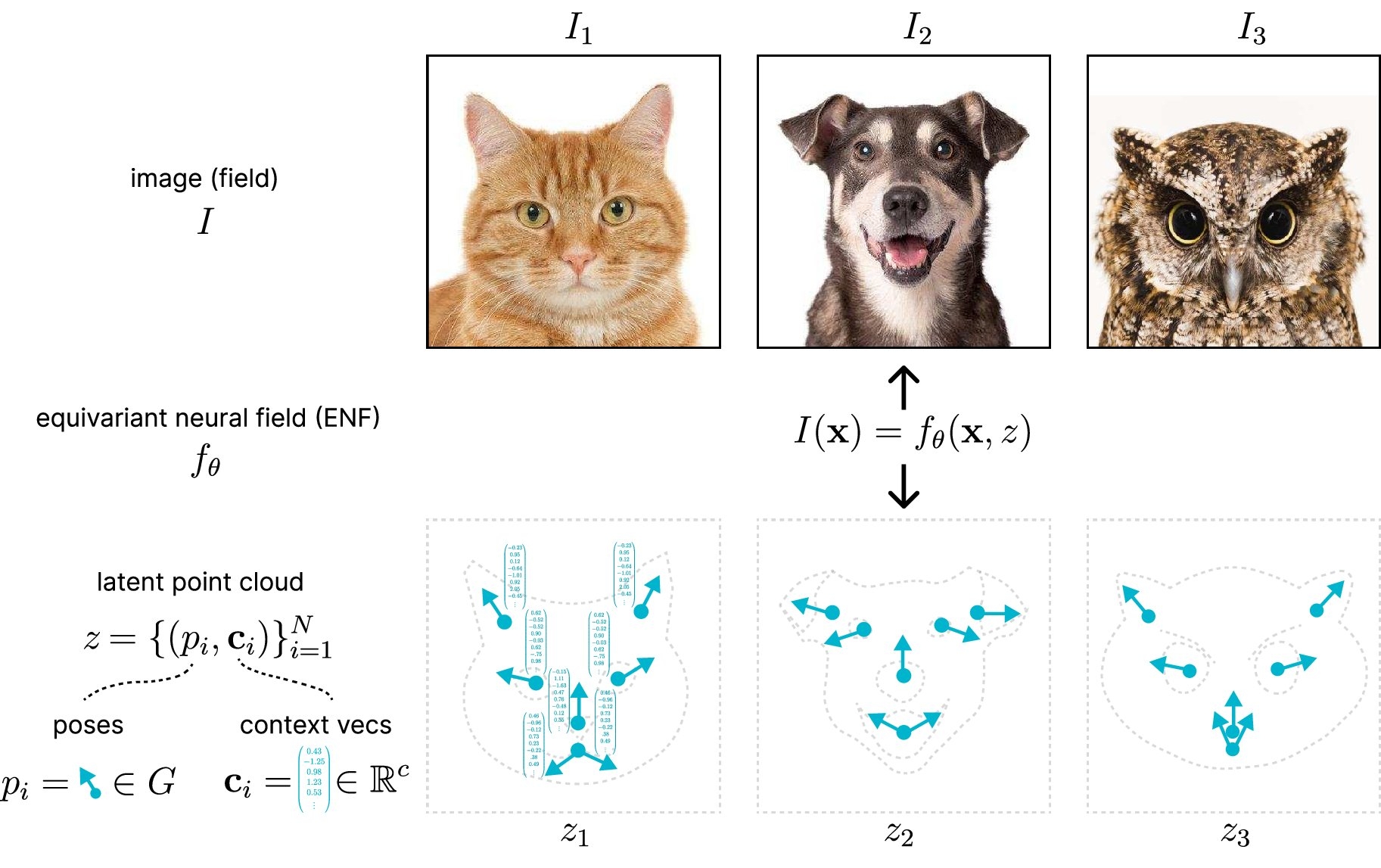
Key Properties of ENFs
- Equivariance: If the field transforms, the latent representation transforms accordingly. This property ensures that the latent space preserves geometric patterns, enabling better geometric reasoning.
- Weight Sharing: ENFs utilize shared weights over similar local patterns, leading to more efficient learning.
- Localized Representations: The latent point sets in ENFs enable localized cross-attention mechanisms, enhancing interpretability and allowing unique field editing capabilities.
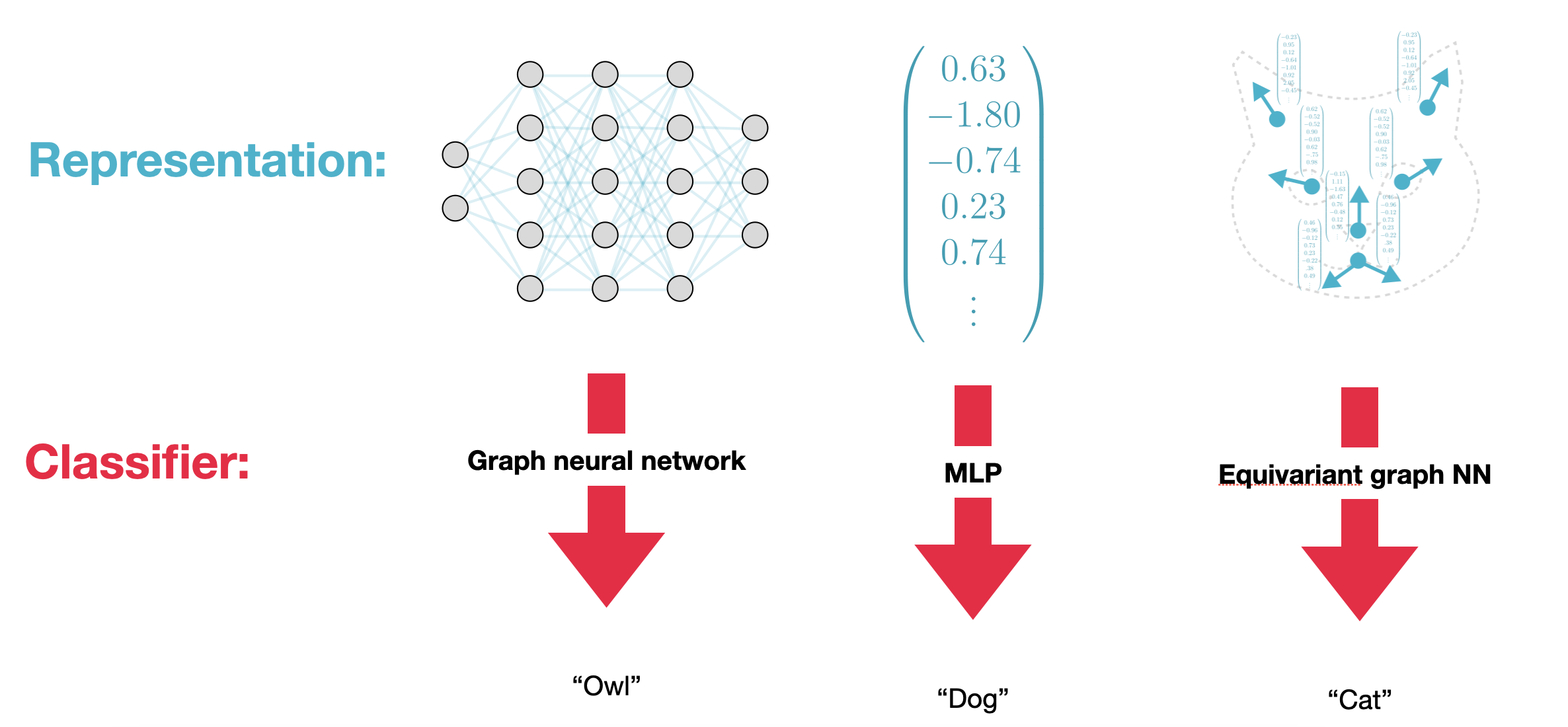
Use of Neural Fields in downstream tasks
As brief interjection, we provide some background on how NeFs are used in downstream tasks. As (a subset of) model NeF parameters are optimized reconstruct specific samples, these parameters may be used as a representation of their corresponding signals. These representations serve as input to downstream models for tasks such as classification, segmentation or even solving partial differential equations.
Methodology
We now delve into the technical details of ENF, focusing on the key components that enable the model to ground continuous representations in geometry.
Requirements for Equivariant Neural Fields
The equivariance or steerability property of ENFs can be formally defined as:
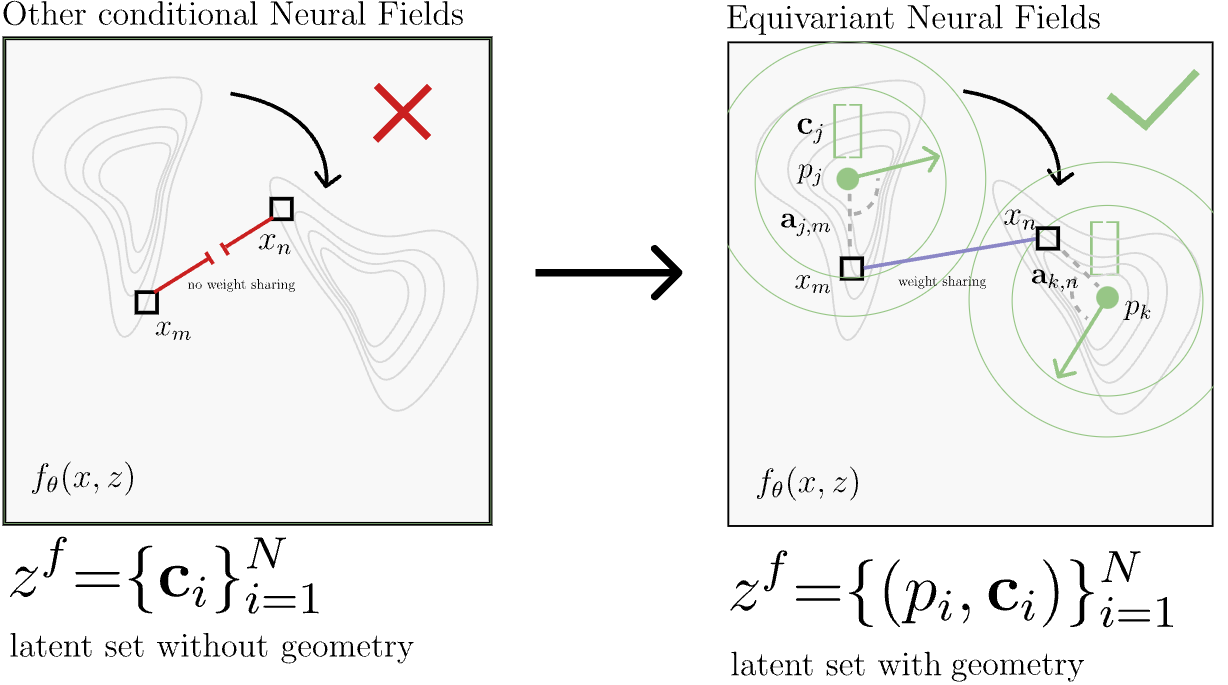
\[\forall g \in G : f_{\theta}(g^{-1}x, z) = f_{\theta}(x, gz).\]This property ensures that if the field as a whole transforms, the latent representation will transform in a consistent manner. This is crucial for maintaining geometric coherence in the latent space. In order reason about the application of a group action on $z$, the authors equip the latent space with a group action by defining $z$ as a set of tuples \((p_i, \mathbf{c}_i)\), where $G$ acts on $z$ by transforming poses \(p_i: gz = \{(gp_i, \mathbf{c}_i)\}_{i=1}^N\).
For a neural field to satisfy the steerability property, the authors show it must be bi-invariant with respect to both coordinates and latents. This means that the field $ f_{\theta} $ must remain unchanged under group transformations applied to both the input coordinates and the latent point cloud, i.e.:
\[\forall g \in G: f_\theta(gx, gz) = f_\theta(x, z).\]This observation is leveraged to define the architecture of ENFs, ensuring that the model is equivariant by design.

Equivariance through Bi-invariant Cross-Attention
ENFs utilize a bi-invariant cross-attention mechanism to parametrize the neural fields in order to achieve the aforementioned steerability property. The cross-attention operation is defined as: $ f_{\theta}(x, z) = \sum_{i=1}^{N} \text{att}(x, z) v(a(x, p_i), c_i) $ where $ a(x, p_i) $ is an invariant pair-wise attribute that captures the geometric relationship between the coordinate $ x $ and the latent pose $ p_i $, ensuring that the cross-attention operation respects the aforementioned bi-invariance condition.
Note that the choice of bi-invariant is related to the choice of group \(G\) and the specific application domain. For example, in natural images \(G\) may be the group of 2D Euclidean transformations, while in 3D shape representations \(G\) may be the group of 3D rigid transformations, leading to different choices of bi-invariant \(a(x, p_i)\). For a better understanding of bi-invariant properties we refer to
Enforcing Locality in Equivariant Neural Fields
To enforce locality, ENFs incorporate a Gaussian window into the attention mechanism. This ensures that each coordinate receives attention primarily from nearby latents, akin to the localized kernels in convolutional networks. This locality improves the interpretability of the latent representations, as specific features can be related to specific latent points $(p_i, \mathbf{c}_i)$. Moreover, locality also improves parameter-efficiency by allowing for weight sharing over similar patterns.

Experimental Validation
The authors validate the properties of ENFs through various experiments on image and shape datasets, providing metrics for reconstruction and downstream classification. Moreover, authors play around with the ENFs latent space to demonstrate the benefits of having a geometrically grounded latent space. A separate study by Knigge et al. demonstrates the use of ENFs in modelling spatiotemporal dynamics.
Image and Shape Reconstruction and Classification
ENFs were evaluated on several image datasets, including CIFAR-10, CelebA, and STL-10. The results show that ENFs achieve higher peak signal-to-noise ratio (PSNR) in image reconstruction tasks compared to CNFs. This improvement is attributed to the geometric grounding and weight-sharing properties of ENFs.
| Model | Symmetry | Cifar10 | CelebA | STL-10 |
|---|---|---|---|---|
| Functa | x | 31.9 | 28.0 | 20.7 |
| ENF - abs pos | x | 31.5 | 16.8 | 22.8 |
| ENF - rel pos | $\mathbb{R}^2$ | 34.8 | 34.6 | 26.8 |
| ENF - abs rel pos | SE(2) | 32.8 | 32.4 | 23.9 |
| ENF - ponita | $\rm SE(2)$ | 33.9 | 32.9 | 25.4 |
For classification, the authors used the latent point sets extracted from the trained ENF models. The classification accuracy on CIFAR-10 shows a significant improvement over conventional CNFs, highlighting the superior representation capabilities of ENFs.
| Model | Symmetry | Cifar10 |
|---|---|---|
| Functa | x | 68.3 |
| ENF - abs pos | x | 68.7 |
| ENF - rel pos | $\mathbb{R}^2$ | 82.1 |
| ENF - abs rel pos | SE(2) | 70.9 |
| ENF - ponita | SE(2) | 81.5 |
The authors also tested ENFs on shape datasets using Signed Distance Functions (SDFs). The results indicate that ENFs can effectively represent geometric shapes with high fidelity, further validating the geometric interpretability of the latent representations.
| Model | Reconstruction IoU (voxel) | Reconstruction IoU (SDF) | Classification |
|---|---|---|---|
| Functa | 99.44 | - | 93.6 |
| ENF | - | 55 | 89 |
Latent Space Editing
The authors demonstrate the benefits of the geometrically grounded latent space in ENFs by performing latent space editing.


Spatiotemporal Dynamics Modelling
Another usecase for ENFs is highlighted in the paper “Space-Time Continuous PDE Forecasting using Equivariant Neural Fields”



Conclusion
Equivariant Neural Fields leverage geometric grounding and equivariance properties to provide continuous signal representations preserving geometric information. This approach opens up new possibilities for tasks that require geometric reasoning and localized representations, such as image and shape analysis, and shows promising results in forecasting spatiotemporal dynamics.
This blog post has explored the foundational concepts and the significant advancements brought forward by Equivariant Neural Fields. By grounding neural fields in geometry and incorporating equivariance properties, ENFs pave the way for more robust and interpretable continuous signal representations. As research in this area progresses, we can expect further innovations that leverage the geometric and localized nature of these fields, unlocking new potentials across diverse applications.